画像 等差数列の和 200299-等差数列の和 小学生
定数数列 定数数列の和は、定数の項数倍。 (1) 等差数列 等差数列 の和は、初項と末項の和に項数を乗じた数の1/2。 (2) 特に、 (3) 証明1 等差数列の 項目までの和を とすると、 (4) 証明2 式()を使って等差×等比型の場合,結果を覚える形にすることはできませんが, 上で示した方法を真似すると 「中間項が消えなくても」「中間項の和が求まるので」 全体の和が求まります。 この場合は, 「中間項が等比数列」となり,和が求まることになります等差数列公式都有哪些 等差数列是常见数列的一种,如果一个数列从第二项起, ;

数学b 数列 1 6 等差数列の和の最大 Youtube
等差数列の和 小学生
等差数列の和 小学生-計算式を用いる 等差数列の和は は = () という公式を用いて求めます。 つまり、等差数列の和は、1つ目の項と最後の項の平均と項数を掛けて算出します。 数列の基本7| 等差×等比型の数列の和は引き算がポイント 等差数列 3, 5, 7, 9, 等比数列 2, 6, 18, 54, を考えます. このような 等差×等比型の数列の初項から第 n 項までの和は, n を使って表すことができます.




等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座
等差数列(とうさすうれつ) ⇒ 初項に一定の数(公差)を加えることで得られる数列 等差数列の一般項を求める式を下記に示します。 等差数列、初項の詳細は下記をご覧ください。 等差数列の公式は?3分でわかる公式、覚え方、等差数列の和の計算一般に,初項 a,公差 d,項数 n の等差数列の末項を としますと,初項から第 n 項までの和 S n は, S n =a(ad)(a2d) (d) (3) となります。また,S 10 は上の例と同様に, S n = (d)(2d) (ad)a (4) と書けますので,(3)と(4)の辺々加えますと,式の左辺は、第1項から第n項までの等差数列の和を表していますね。 一方、 第n項までの等差数列の和 は、公式より 2(a 1 a n )/n でしたね。 これがポイントにおける右辺の式になっています。
公差が正である時には、等差数列の和は無限に増え続けてしまい、最大値は存在しません。また、初項も公差も負である時には、初項を最大値として和は減り続けてしまいます。 「a 1 が正で、公差dが負の時」 という条件が重要なのですね。一般に,数列 a 1,a 2,a 3,,a n, の各項に,一定の数 d を加えると次の項が得られるとき, a n1 =a n d つまり a n1a n =d という関係が成り立ちます。この関係が成り立つ数列を 等差数列 と呼び d を 公差 と呼びます。上の例では,初項 1,公差 3 の等差数列となります。等差数列求和计算器 本工具用于计算一个等差数列n项的总和,并找出第n项的算术。 一个级数是一连串的数字,根据一定规则形成一定的顺序排列。 而如果一个级数里的每个项跟前一个项相差一个常数,那么这样的级数被称为算术级数和常数不同的AP称为常见
等差数列の和(Sn)を等差級数といい、次式の公式となる。 Sn = a1 a2 ・・・ an = n(a1an)/2 = 2n{ 2a1 (n1)d } たった1日で即戦力になるExcelの教科書 入門者のExcel VBA―初めての人にベストな学び方 (ブルーバックス) Excel VBAのプログラミングのツボとコツがゼッタイにわかる本 等比数列 2,4,8,16,32,64なお、エクセルで等差数列の和を計算するときは、わざわざこの等差数列の和の公式を利用しなくても、一般項を単純にすべて足し合わせることで計算可能です。 以下で、詳細の手順を確認していきます。 関連記事 エクセルで等比数列の計算を行う方法 エクセルで等差数列の和を求める 自然数の和の公式だけ覚えていれば等差数列の和の公式を瞬時に導出できます! 導出 S = a ( a d ) ( a 2 d ) ⋯ { a ( n − 1 ) d } S=a(ad)(a2d)\cdots \{a(n1)d\} S = a ( a d ) ( a 2 d ) ⋯ { a ( n − 1 ) d }




高校数学b 等差数列を利用する倍数の和 受験の月



数列と級数 Of 京極一樹の数学塾会員頁
等差数列の和の公式 初項 \( a \),公差 \( d \),末項 \( l \),項数 \( n \) の等差数列の和を \( S_n \) とすると \( \displaystyle \large{ \color{red}{ S_n = \frac{1}{2} n (a l) } } \) \( \displaystyle \large{ \color{red}{ S_n = \frac{1}{2} n \left\{ 2a (n1) d \right\} } } \)等差数列の和の公式と求め方まとめ 一般項・和の公式について問題を解きながら見てきました。 an=a1+ (n-1)dと表せる。 1/2×n×(a+l)と表せる。 1/2×n× {2a (n-1)d}と表せる。 これは数列の基本なのでしっかりとマスターしましょう。 等比数列は次に 如果等差数列的公差 \(d0\) ,正数之和一定为正,并且只要是正数,则正数相加的个数越多,其和越大; ↩︎



48s96ub7b0z5f Net Touhisuuretsu




この S とsn ってなんの違いがあるんですか 末項なのか公差の違いですか Clear
数列 序列是一组顺序排列的东西,若这些东西是数,我们便称之为数列。 等差数列 在等差数列里, 每一项和下一项的差是等差数列の応用 問題 1260 以下の整数のうち, 7 で割り切れる数の和を求めよ. 答 S = 方針 等差数列の一般項の公式より, 初項を a 1 ,交差を d 、 一般項を a n とする. a n = a 1 (n − 1) d を用いる. 次に初項から末項までの和 S l は,等差数列の和 等差数列求和公式及推导方法 等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列,常用A、P表示。 这个常数叫做等差数列的公差。 前n项和公式为:Sn=a1*n n* (n1)*d/2或Sn= n* (a1an)/2。
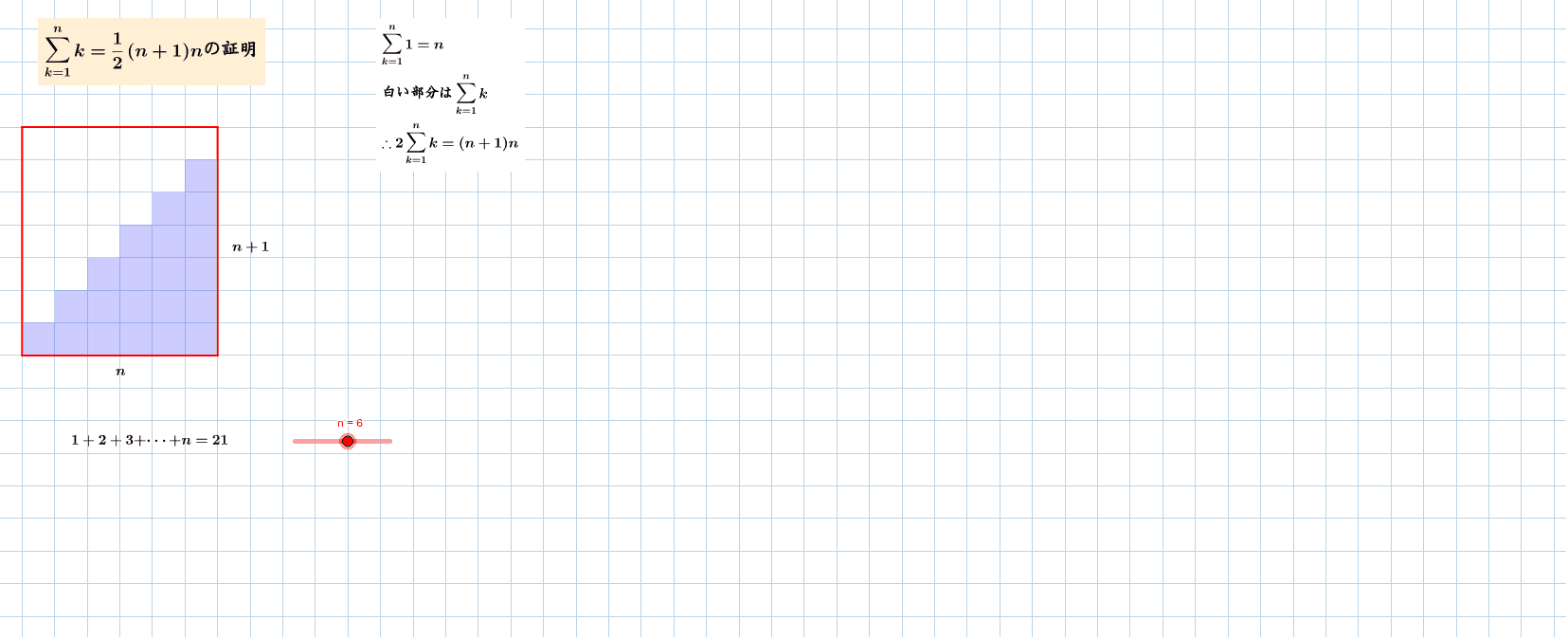



等差数列の和 Geogebra




等差数列の和の最大 数学b 等差数列と等比数列 5 Youtube
等差数列和 一個等差數列的首 n 項之和,稱為等差数列和(sum of arithmetic sequence)或算術級數(arithmetic series),記作 S n 。 舉例來說,等差數列 {1, 3, 5, 7} 的和是 1 3 5 7 = 16 。 等差數列求和的公式如下:この総面積が等差数列の和になるはずです.これを求めるためには,同じものを上に足して2で割ればいいはずです. 長方形の面積 $(a_{1}a_{n})n$ を出して $2$ で割ればいいので,等差数列の和の公式は以下になります( $d < 0$ のときも同じでしょう).という公式が成り立ちます.等比数列をずっとずっと足しあわせていったら, 上の式の右辺になるというのです. 無限に足しあわせたのに一定の値になる(収束する)というのはちょっとフシギな感じがします. 導きかた この公式を導くのは簡単です.等比数列の和の公式 を思い出します




等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座




基本 等差数列の和の公式 初項と公差 数列1 11 Youtube
こんにちは。 da Vinch (@mathsouko_vinch)です。 等差数列の和 等差数列は隣り合う項の差が等しい数列でした。では初項からある任意の項までの和を簡単に計算する術はあるのでしょうか。 まず、次の数列を考えるとこれは 等差数列の和を求める公式 等差数列の初項からある項までをすべて足し合わせる公式がある。 初項a、末項l、項数nの等差数列の和S n を求める公式は以下。 この公式についても具体的な数列を使いながら証明していきたい。 <公式の証明> 数列の代表例その2ポイント (等差)× (等比)の和, (2次式)× (等比)の和の解き方 和を書き並べて, 和から和に公比をかけたものを右にずらして引く. 公比をかけて右にずらして引くという操作は, 等比数列の和の公式 を導くときにもしたことですね. 下の例題と練習問題




等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ




Senior High数学的詳説 数学b 等差数列 等比数列 筆記 Clear
等差数列の和の公式 (A) 初項 a ,末項 l ,項数 n の等差数列の初項から末項までの和 S n は (B) 初項 a ,公差 d ,項数 n の等差数列の初項から第n項までの和 S n は ※どちらも アン( a, n )は必須 デル( d, l )は1つ選びます.等差数列の和の公式が覚えれないよって方は \(S_n=\frac{1}{2}n(al)\) だけ覚えておけば大丈夫ですね! なんで、こんな公式で等差数列の和が求まるの?? という疑問を抱いてしまった方に向けて「公式のなぜ?」についても解説しておきます。 文字を使って考えてしまうと複雑に見えちゃうので等差数列の和を求める公式の証明 初項がa、公差がdの等差数列において、初項から第n項までの和は、 で求めることができます。今回はこの公式を証明します。 証明 証明の方法を理解するために、まずは具体的な数字の入った数列を例に考えていく。




3分でわかる 等差数列の公式をわかりやすく 合格サプリ



等差数列 等比数列 階差数列の公式まとめ 数列
等差数列的判定 (1)a(n1)a(n)=d (d为常数、n ∈N*)或a(n)a(n1)=d,n ∈N*,n ≥2,d是常数等价于{a(n)}成等差数列。 即,若项数为奇数,和等于中间项的2倍,另见,等差中项。 查看更多知识内容,欢迎关注微信公众号数学大师(ID:shuxueds) 返回搜狐,查看更多 责任编辑: 声明:该文观点仅等差数列の総和を等差級数と言い、通例有限算術数列の和を算術級数と言う 。 公差 d の等差数列の n 個の項 a 1 , a 2 , , a n の総和は、 S n = ∑ k = 1 n a k = a 1 a 2 ⋯ a n = n ( a 1 a n ) 2 = n 2 a 1 ( n − 1 ) d 2 {\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}=a_{1}a_{2}\dots a_{n}={\frac {n(a_{1}a_{n})}{2}}={\frac {n2a_{1}(n1)d}{2}}}等差数列(とうさすうれつ)の一般項を求める公式は「an=a (n-1)d」です。 また、等差数列の和の公式はn (aan)/2で算定されます。 anはn番目の項、dは公差、aは初項です。 公差とは等差数列における一定の数dです。 今回は等差数列の公式、覚え方、等差数列の和の計算について説明します。 公差の意味は下記が参考になります。 公差とは? 1分でわかる意味




3講 等差数列の和 1節 等差数列と等比数列 問題集 3章 数列




Excel エクセルで等差数列の和を計算する方法
前回 https//googl/LFNGHA 次回 https//googl/O1NiMG動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が等差数列の和 1からウン千までのランダムな整数を並べたデータに、被りや欠落が無いかを確認するために利用させていただきました。 お年玉 (年齢×1000)の総額計算に! 1から397までの和を求めるため、等差数列計算を利用。 等差数列をなす3つの数をもとめるため。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 アンケートは下記にお等差数列 14, 21, 28, 35, 42, ⋅ ⋅ ⋅ の一般項 a n 、初項から第15項までの和 S 15 を求めよ。 答 S 15 = 945 方針 等差数列の一般項の公式より、 初項を a 1 、交差を d 、 一般項を a n とする。 a n = a 1 (n − 1) d を用いる. 次に初項から第15項までの和 S 15 は




高校数学b 等差数列と等比数列の共通項の数列の一般項 受験の月
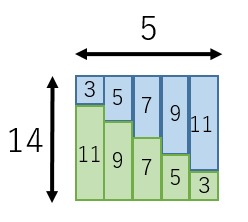



等差数列の和を計算する2つの公式 具体例で学ぶ数学
等差数列の一般項は\(\small{ \ a_n=pnq \ }\)のような \(\small{ \ n \ }\)の一次式 になり、和は\(\small{ \ \mathrm{S}_n=p'n^2q'n \ }\)のような \(\small{ \ n \ }\)の定数項を除く二次式 になるから覚えておこう。 等差数列の一般項 等差数列 とは 隣り合う各項の差が一定 の数列だから、その差を\(\small{ \ d \ 等差数列 例: 2 4 6 ⋯ 100 = 2550 246\cdots 100=2550 2 4 6 ⋯ 100 = 2550 初項が a a a ,末項が l l l ,項数が n n n であるような等差数列の和は, 1 2 n ( a l ) \dfrac{1}{2}n(al) 2 1 n ( a l ) →等差数列の和の公式の例題と証明など 等差数列の和の公式 等差数列の和 S n = ∑ i = 1 n a i は以下のように書き換えられる。 (2) S n = 1 2 n ( a 1 a n) これが等差数列の和の公式だ。 ガウス君の問題だと、 n = 100, a 1 = 1, a 100 = 100 なので、 S 100 = 1 2 100 × ( 1 100) = 5050 というように、公式 (2)を使えば、この問題は瞬殺できる。 天才ガウス君は前提知識なしでこの公式を瞬時にイメージすることができ




数学b 数列 1 6 等差数列の和の最大 Youtube



等差数列をグラフにしてみよう 父ちゃんが教えたるっ
等差数列の和の公式 さて、最後は「等差数列の和」を求める公式です。 まずは、以下の数列で考えていきましょう。 1, 3, 5, 7, 9, 11, 13, 15, 17 これは初項1、公差2の等差数列です。 この9つの項の和(今後sと表します)を求めるには、どうしたらいいの
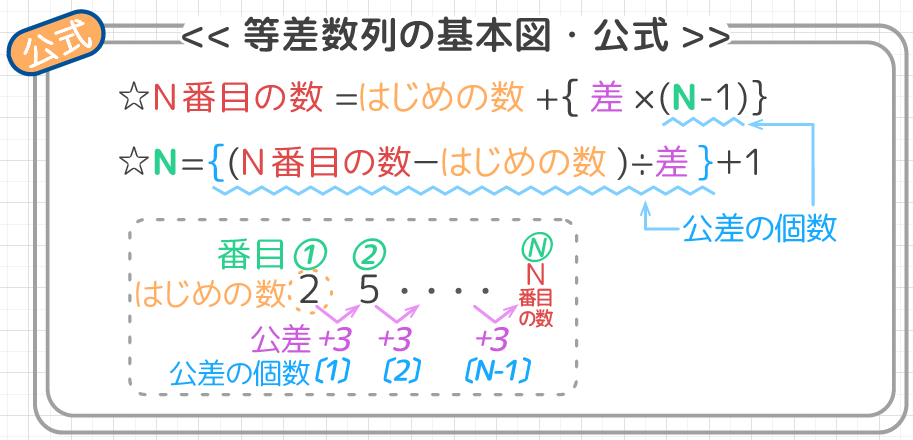



中学受験 差 階差数列 を利用する問題の解き方 無料プリントあり そうちゃ式 受験算数 新1号館




数学の天才 ガウス少年 等差数列の和の公式の考え方 スモビュ




10 4 N S N Descubre Como Resolverlo En Qanda



数学の質問です 等差数列の和の公式二つ 写真で色ペンで線が引いてあるもの Yahoo 知恵袋




等差数列の性質と一般項と和の公式 等差数列の和は台形の面積 Irohabook




高校数学の等差数列の和の問題を学び直し 大学受験対策にも タロウ岩井の数学と英語 Note




等差数列の奇数の和の求め方が分かりません 教えてください Clear




2 Left Anright 1n Sn A3 Descubre Como Resolverlo En Qanda




高校数学b 等比数列の一般項 A N Ar N 1 受験の月




等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ
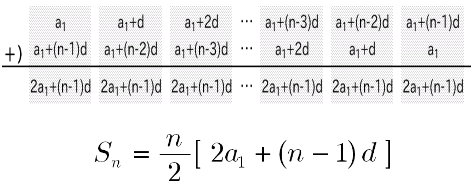



数列 等差数列の和を求める 大人が学び直す数学




3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ



倍数の和 等差数列の利用 大学受験の王道




5分間studying 数列 3 等差数列の和 数 Bを ぶっ飛ばせ



1




等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8




等差数列の一般項と和 おいしい数学




数学 等差数列の和の公式 の導出と 自然数の和 を求めてみたよ 数学おじさん Oj3 Math Youtube




等差数列 数学の偏差値を上げて合格を目指す




漸化式の基本2 漸化式の基本の 等差数列 と 等比数列



等差数列の和を再帰を使って求める関数です 等差数列の和の Yahoo 知恵袋




なぜnー1何ですか N 1ではないんですか 階差数列だからですか Clear



等差数列の和の問題について




数列の和 小学生でもわかる等差数列の和 東進衛星予備校 名古屋新瑞橋校のブログ




等差 等比 の和 2次式 等比 の和 おいしい数学



等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8



等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ




等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ



等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ




高校数学b 等比数列 A N の和 1 映像授業のtry It トライイット




等差数列の一般項と和 おいしい数学



等差数列の和



階差数列



数列と級数 京極一樹の数学塾




高校生 等差数列の和のノート一覧 Clear



問題3 等差数列の和の最大値 鳩場 通弘




数列の基本2 等差数列の和の公式 と 等比数列の和の公式




高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月




3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ




高校数学b 等差数列 A N の和 1 映像授業のtry It トライイット




等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
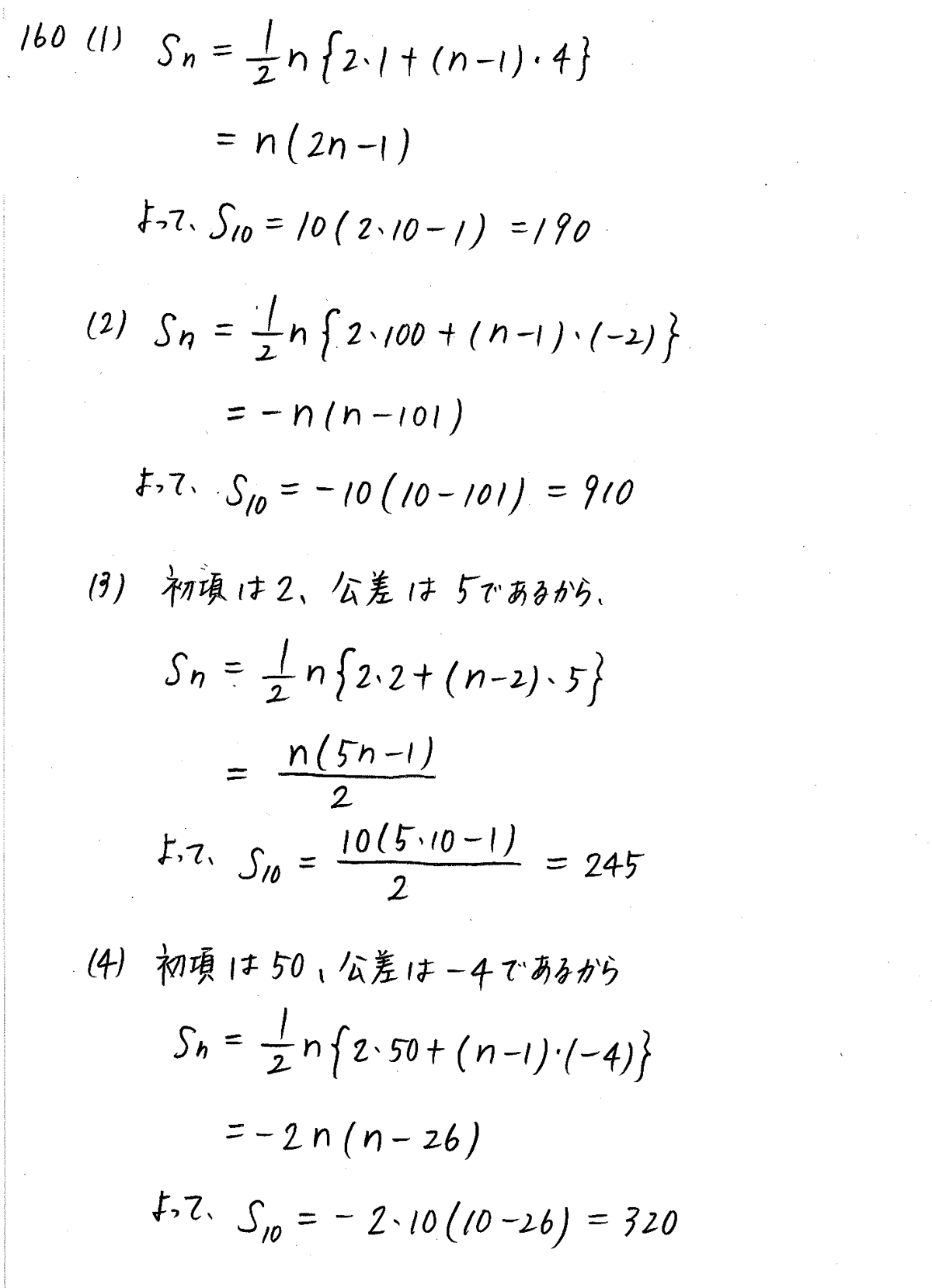



クリアー数学b 数b P137 15 等差数列の和



タロウ岩井の数学と英語 Noteの補足など 高校数学の等差数列の和を学び直し Powered By Line
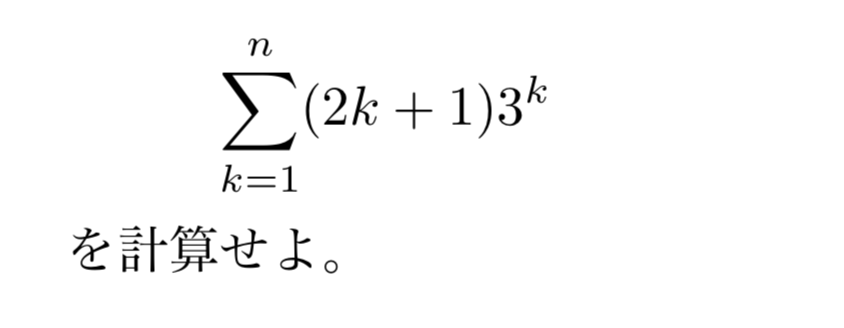



和の中抜けとは 分数や連続整数の積の総和を求める方法を例題付きで紹介 東大医学部生の相談室




等差 等比 の和 2次式 等比 の和 おいしい数学




3分でわかる 等差数列の公式をわかりやすく 合格サプリ




高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット




高校数学b 等差数列の和の公式 S N 1 2n A L 受験の月



等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典




みんなの算数オンライン 教科書 等差数列の和
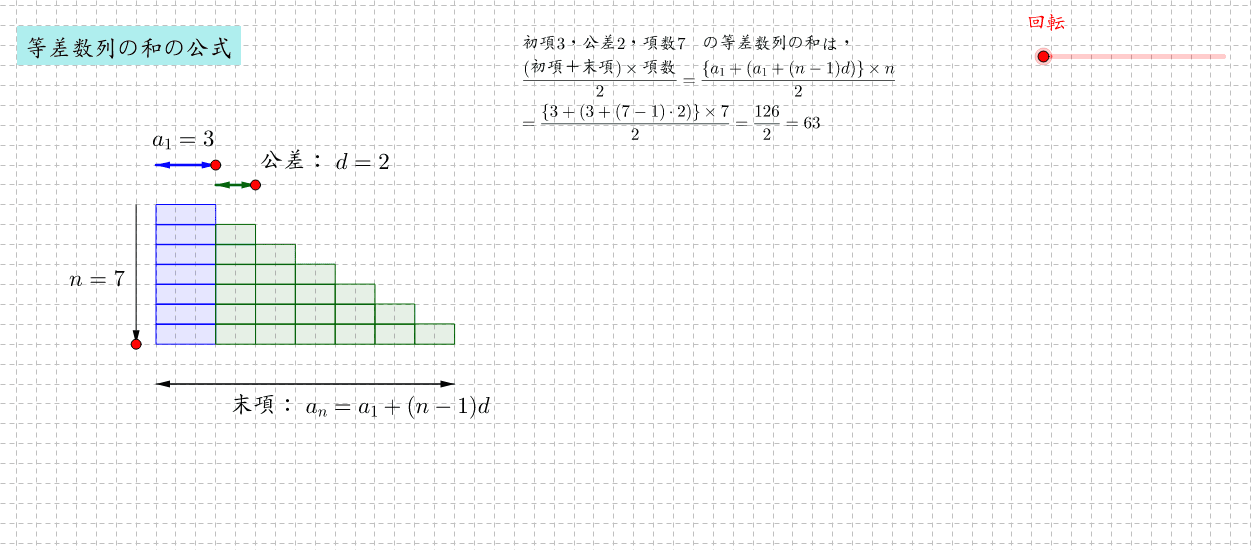



等差数列の和 Geogebra




等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ



1 1 5 9 3 49 2 2 7 1 Descubre Como Resolverlo En Qanda




等差 等比 の和 2次式 等比 の和 おいしい数学



1




等比数列の一般項と和 おいしい数学



誤答から学ぼうシリーズ 等差数列 等比数列 型の数列の和 ほのぼの数学頑張ろう
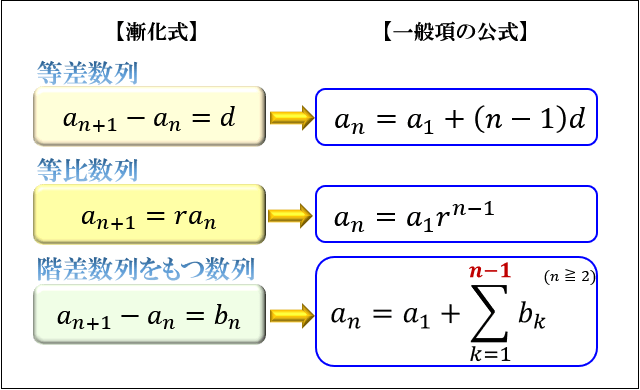



漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ



Doとwhileを使って初期値a 10と公差b 5としてiが0から9番目まで Yahoo 知恵袋




等差数列の和 sₙ a aₙ n ワンセンテンス算数 Note



48s96ub7b0z5f Net Tousakakerutouhi




高校数学b 等差数列 A N の和 1 映像授業のtry It トライイット




高校数学b 等差数列の和s Nの最大 最小 受験の月




等差数列の和 23から57までの奇数の和 Clear



等差数列 等比数列 の和で和s 1 1 2 4 3 Yahoo 知恵袋




等差数列の一般項や和の公式をマスターしよう ますますmathが好きになる 魔法の数学ノート




等差数列 等比数列の形の数列の和 高校数学 身勝手な主張




等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8



等差数列の和の公式で 写真のような公式があると思いますが これの Yahoo 知恵袋




B 数列 1 2 等差数列の和の最大値 標準 Youtube



48s96ub7b0z5f Net Tousa Suuretsu




数列 奇数の和 を求める 大人が学び直す数学




力をつけよう2 S 等差数列 等比数列 力をつけていいんじゃない




等差数列の和の公式の証明を超分かりやすく解説するよ



3




最後のオカキの質問です どうして等差数列の和の形になっているので 数学 教えて Goo




等差数列 等比数列 優技録



等差数列と等比数列の積の和の問題の解法ポイント 数列




例題で学ぶ高校数学 等差数列 等比数列 型の数列




階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ



1
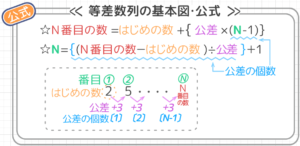



無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館




高校生 数学b 東京書籍 01 1章1節数列 等差数列の和 教科書解答解説 赤城 ᐡᐤᐡ




高校数学 B 数列 7歳の子が考えた等差数列の和を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学




等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



等差 等比型


コメント
コメントを投稿